
You will learn to calculate the ratio of the length. So remember these two key things, when you are looking at your test or your quiz. You will learn to use the properties of similar right triangles in practice. So how many similar triangles have you created? We have three triangles that are all similar to each other. And I'm going to use two different markings. Not only do both of these triangles have a right angle, but they share this angle in the corner. The same thing can apply to this triangle on the right. Now, what does that do for us Well, that tells us that the ratio of corresponding sides are going to be the same. And then, vertex B right over here corresponds to vertex D. So if I look at this large triangle and I count that as triangle number 1, this is triangle number 2 and this is triangle number 3, I see that comparing triangle number 1 which is the large one, I have one right angle in each of these, and they share this angle right there which means you can use your angle angle shortcut to say that theses two triangles must be similar. So we know triangle ABC is similar to triangle- so this vertex A corresponds to vertex E over here.

So I had created one triangle and the left side of that altitude and on the right side I've created another smaller triangle. I'm going to redraw the two triangles that I've created down below. What I'm going to do is I'm going to create a certain number of similar triangles. And that is if I have a right triangle and if from this right angle, if I dropped an altitude to the other side.
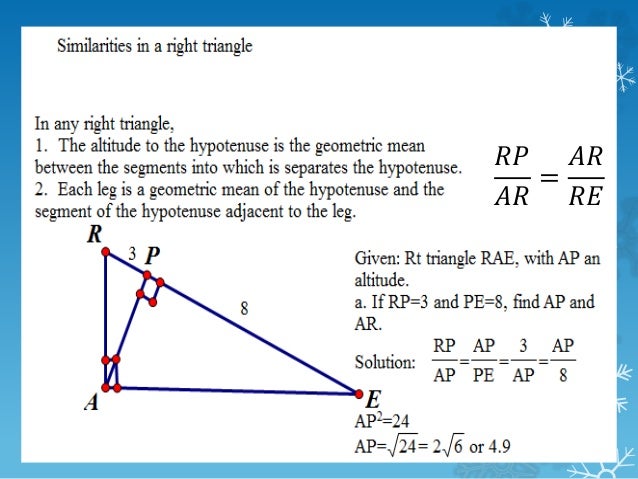
So if you see a problem like this and you're trying to find some of your side lengths, you know that you have similar triangles so you can set up proportions. So we have angle angle angle as congruent between these two triangles. And last we have vertical angles, which means that these two must be congruent as well. The altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle. The same could be said for these angles up here. So if these two have the exact same intercepted arc, then they must be congruent. Now there's another angle that has the exact same end points. The intercepted arc extends from one point to the other. If I pick one of these angles here, and I looked at the endpoints well that would be one endpoint right here, and one endpoint right there. Well let's go back to what we know about inscribed angles in a circle. Similar right triangles (179.If you see a problem that looks like this, the question is do we have similar triangles. Similar triangles (740.4 KiB, 2,462 hits) Similar Right triangles: Two right triangles are similar if the corresponding sides are proportional to each other, and the corresponding angles are congruent. It follows that $\alpha = \beta$, which means that triangles $ABC$ and $GHJ$ are thus similar by the SSA theorem. The opposite angle to the side of the longest length in triangle $ABC $is $\alpha$ and opposite angle to the longest side in triangle $GHJ$ is $\beta$. We will expand segment lines $\overline,$$ So how can we construct a similar triangle? Lets put that into words: in any two similar right triangles, the ratio of a leg to the hypotenuse of one triangle is equal to the ratio of the corresponding. The right-angled triangles have a common thing which is their 90. Two triangles are similar if their two corresponding angles are congruent. It is one of the most fundamental concepts of geometry, and further, the concept of Similarity. There are four theorems that we can use to determine if two triangles are similar. Since the triangles are similar, side proportions can be used to find the lengths of any missing lengths or altitude. Two triangles $ABC$ and $DEF$ are similar, thus we write: $\bigtriangleup ABC \sim \bigtriangleup DEF$. Theorem: If the altitude is drawn to the hypotenuse of a right triangle, then the two triangles formed are similar to the original triangle and to each other. Similarity is the relation of equivalence. Investigate the relationships between the altitude drawn from the right angle and perpendicular to the. In similarity, angles must be of equal measure with all sides proportional. Similar Right Triangles: The Altitude to the Hypotenuse.
We already learned about congruence, where all sides must be of equal length. Triangle similarity is another relation two triangles may have. Before trying to understand similarity of triangles it is very important to understand the concept of proportions and ratios, because similarity is based entirely on these principles. This investigation is a great demonstration to help students visualize similar right triangles To begin, start with a regular sheet of paper.


 0 kommentar(er)
0 kommentar(er)
